第九课 立体几何
注:所有立体几何图片均来源于高中数学书A版必修2
1. 斜二测画法(画直观图)
常令坐标轴的夹角为 45°,遵循横不变,纵减半的原则,如图
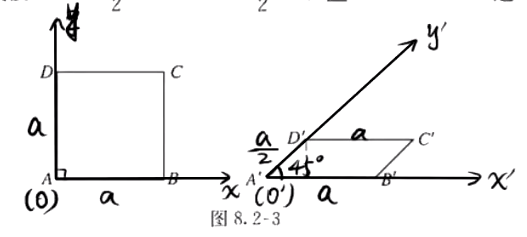
面积关系:S′=42S
2. 常用基本事实
-
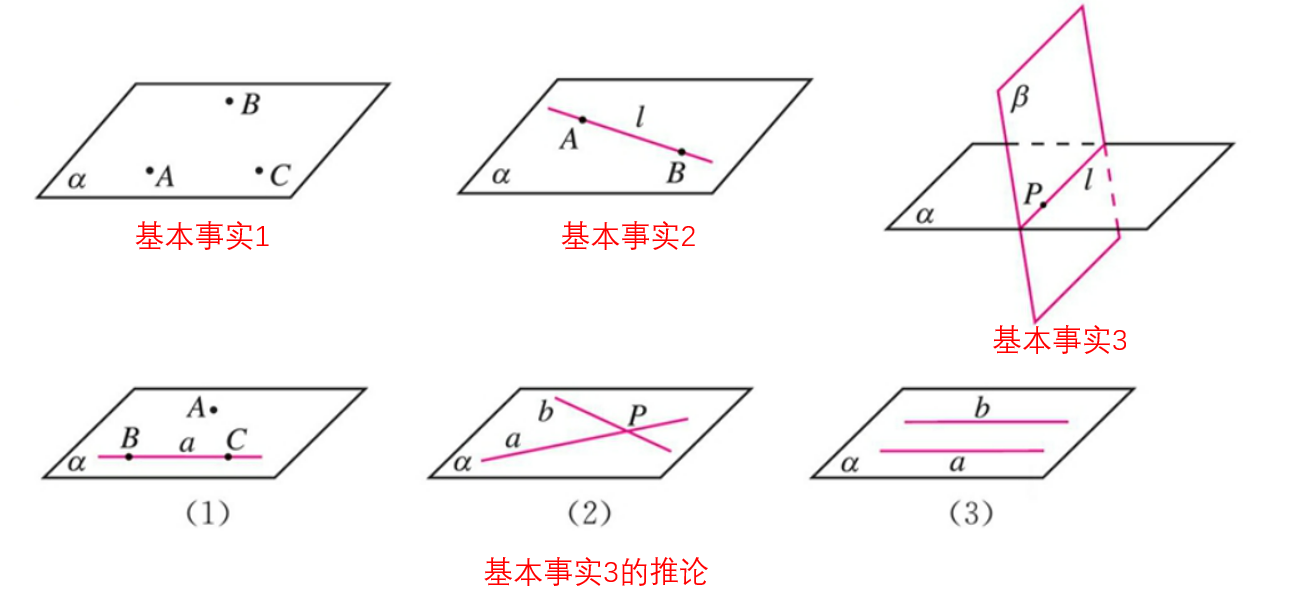
基本事实1
过不在一条直线上的三个点,有且只有一个平面
A,B,C 三点不共线 且 A,B,C∈α ⇒ α 唯一
-
基本事实2
如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内
A∈l,B∈l 且 A∈α,B∈α ⇒ l⊏α
-
基本事实3
如果两个不重合的平面有一个公共点,那么它们有且只有一条经过该点的公共直线
P∈α,Q∈β 且 α,β 不重合 ⇒ α∩β=l 且 l 唯一
-
推论1
经过一条直线和这条直线外一点,有且只有一个平面
-
推论2
经过两条相交直线,有且只有一个平面
-
推论3
经过两条平行直线,有且只有一个平面
-
基本事实4
平行于同一直线的两直线平行
a//b 且 c//b ⇒ a//c
3. 位置关系
-
直线与直线的位置关系
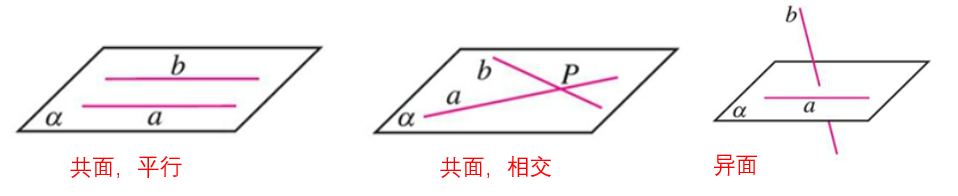
- 共面直线
- 相交:a∩b=P
- 平行:a//b
- 异面直线:不在任何一个平面内的两条直线
-
直线与平面的位置关系
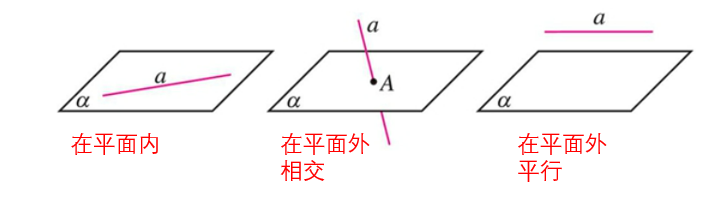
- 直线在平面内:a⊏α
- 直线在平面外
- 相交:a∩b=P
- 平行:a//α
-
平面与平面的位置关系
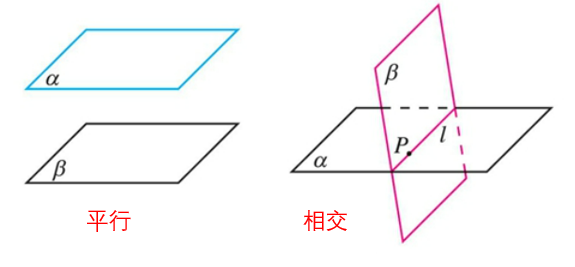
- 相交:α∩β=l
- 平行:α//β
4. 判定定理与性质定理
-
直线与平面平行的判定定理与性质定理
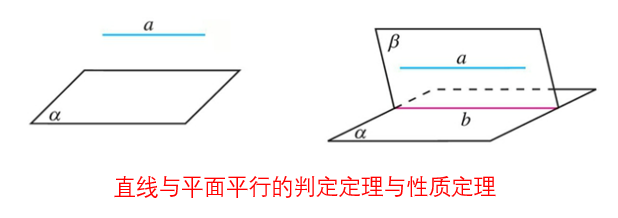
- 判定:a//b 且 b⊏α 且 a⊏α ⇒ a//α
- 性质:a//α 且 a∈β 且 α∩β=b⇒ a//b
-
平面与平面平行的判定定理与性质定理
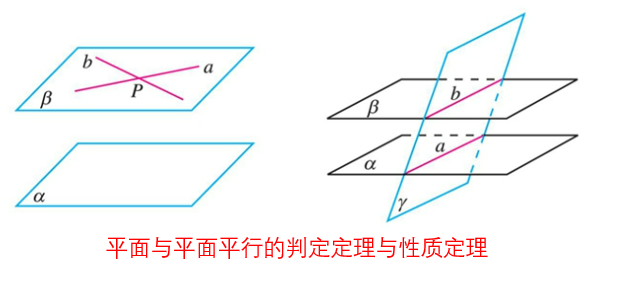
- 判定:a//α 且 b//α 且 a∩b=P 且 a∈β 且 b∈β ⇒ α//β
- 性质:α//β 且 α∩r=a 且 β∩r=b ⇒ a//b
-
直线与平面垂直的判定定理及性质定理
- 判定:l⊥a 且 l⊥b 且 a∩b=P 且 a,b⊏α ⇒ l⊥α






