高中数学笔记-6-三角函数
第六课 三角函数
1 | |
1. 任意角与弧度制
-
度量角的大小
角度制、弧度制
对于角度制的 ,它所对的弧度制 满足:
在一个半径为 ,圆心角为 的扇形中,弧度制的表示就是弧长比半径
单位:
一弧度:长度等于半径长的弧所对的圆心角
在坐标系上表示角:始边为 轴正半轴,将其逆时针旋转 度,得到终边
终边与 相同的角:
-
角的分类
类别 解释 正角 顺时针旋转 负角 逆时针旋转 零角 无旋转 类别 集合 象限角 第一象限角 第二象限角 第三象限角 第四象限角 轴线角 终边在坐标轴 终边在 轴 终边在 轴正半轴 终边在 轴负半轴 终边在 轴 终边在 轴正半轴 终边在 轴负半轴 -
扇形
弧长公式:
面积公式:
2. 三角函数
-
定义
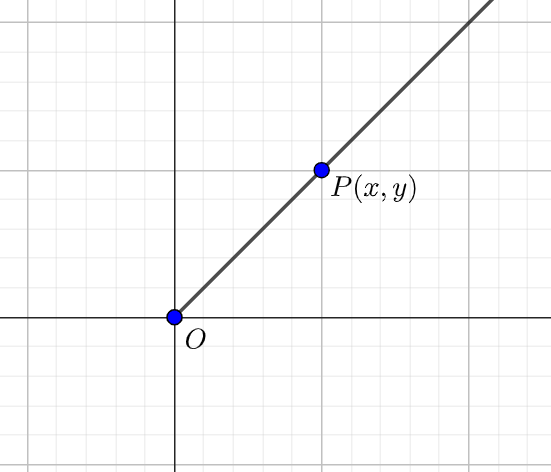
如图,令
名称 定义 在单位圆上 正弦 余弦 正切 -
定义域和符号
三角函数 定义域 第一象限 第二象限 第三象限 第四象限 记忆方法:ASTC(正二切三余四全一)
象限 口诀 解释 第一象限 A 第一象限三个函数全正(All) 第二象限 S 第二象限 为正 第三象限 T 第三象限 为正 第四象限 C 第四象限 为正 -
同角三角函数之间的关系(切化弦,弦化切)
平方关系:
商数关系:
例题:若 ,则 的值为?
答案
由题目得
即
原式
-
诱导公式
公式一 公式二 公式三 公式四 公式五 公式六 口诀:奇变偶不变,符号看象限
口诀 解释 奇 的奇数倍 偶 的偶数倍 变 改变函数名 符号看象限 把 当锐角,代入左边的式子,判断正负 例题:
答案
原式
-
图像与性质
图像 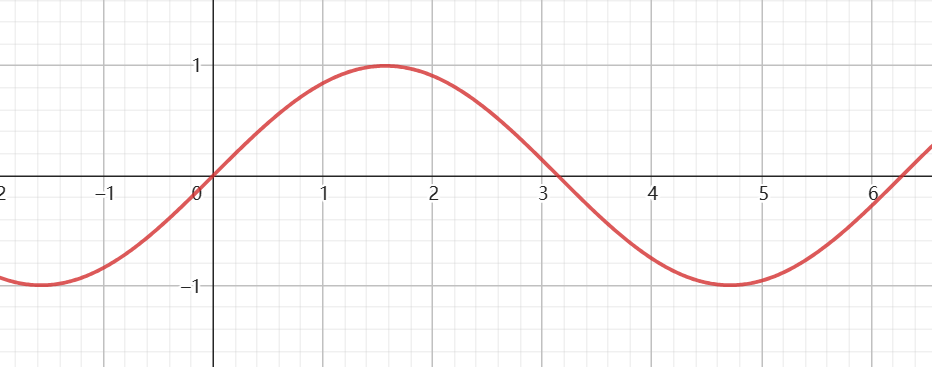
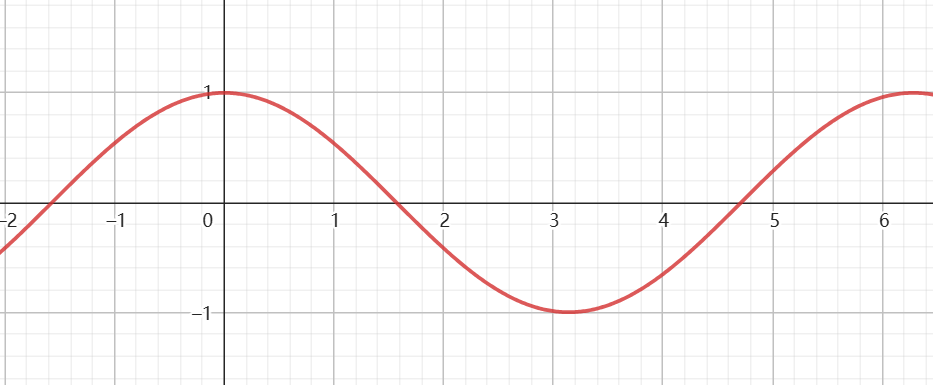
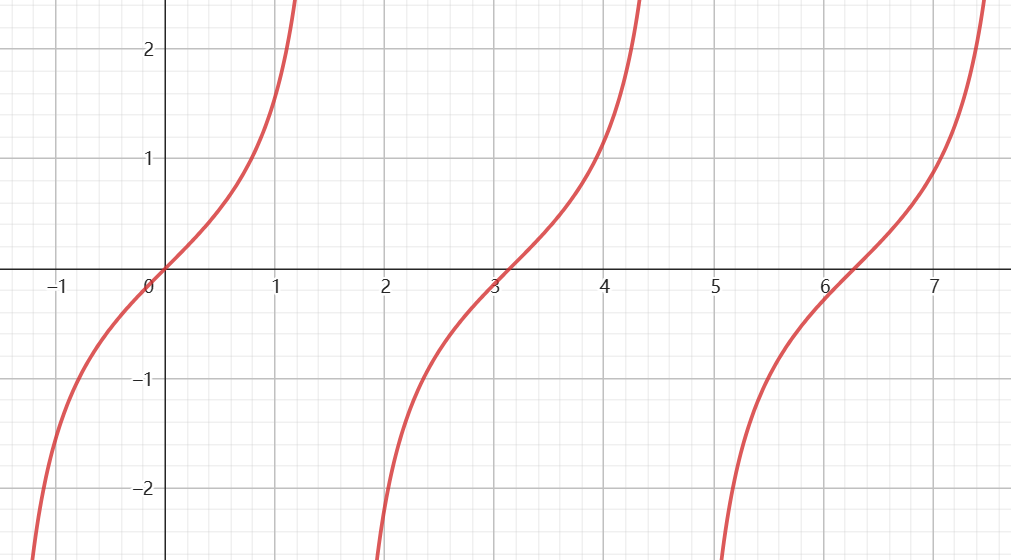
定义域 值域 最值 当 时
当 时当 时
当 时周期性 周期:
最小正周期:
:周期:
最小正周期:
:周期:
最小正周期:
:奇偶性 奇函数 偶函数 奇函数 奇偶性 若 是奇函数,则
若 是偶函数,则若 是奇函数,则
若 是偶函数,则单调性 递增区间:
递减区间:递增区间:
递减区间:递增区间: 对称性 对称轴:
对称中心:对称轴:
对称中心:无对称轴
对称中心: -
图像变换
例:从 到
从 到 操作 纵坐标伸长到原来的 倍 横坐标缩短到原来的 倍 向左平移 个单位(左加右减) 向上平移 个单位(上加下减) 和 同理
例题:为了得到函数 的图像,只需把函数 的图像( )
A. 向左平移 个单位 B. 向右平移 个单位
C. 向左平移 个单位 D. 向右平移 个单位
答案
统一函数名:
由 到 :向右平移 个单位
故选B
3. 三角函数公式
-
和差角公式
-
二倍角公式(升幂缩角)
-
降幂公式
-
辅助角公式
其中 ,
-
常见的三角不等式
若 ,则
若 ,则
-
积化和差公式
-
和差化积公式
口诀:正加正,正在前;正减正,余在前;余加余,两条余;余减余,余不见,符号很讨厌
高中数学笔记-6-三角函数
http://shicj.pages.dev/2024/11/09/高中数学笔记-6-三角函数/