P5597 【XR-4】复读 题解
一道思维题,我自己没能想出来,研究了很久,最后参考了题解想了很久才做出来,但题解写得比较简略,于是在此记录一下。
解题思路
-
因为是无限延伸的完全二叉树,所以只要不对树根进行U操作,所有的命令都是合法的。
-
因为是无限复读指令,所以每一次执行指令之后的相对的位移是一样的。
-
于是,可以将要遍历的整棵树分成几个相同(也可以有包含关系)且连续的部分(这样可以用重复执行相同指令串来处理),然后处理每一个部分的过程就是要求出的指令串。
-
每一部分的具体操作中一定会遍历起点到终点的边一遍和其他的边两遍,于是有 $tot = 2 \times ( sum - 1 ) - d $( 是步骤数, 是点数, 是起点到终点的边数),具体参考图片:
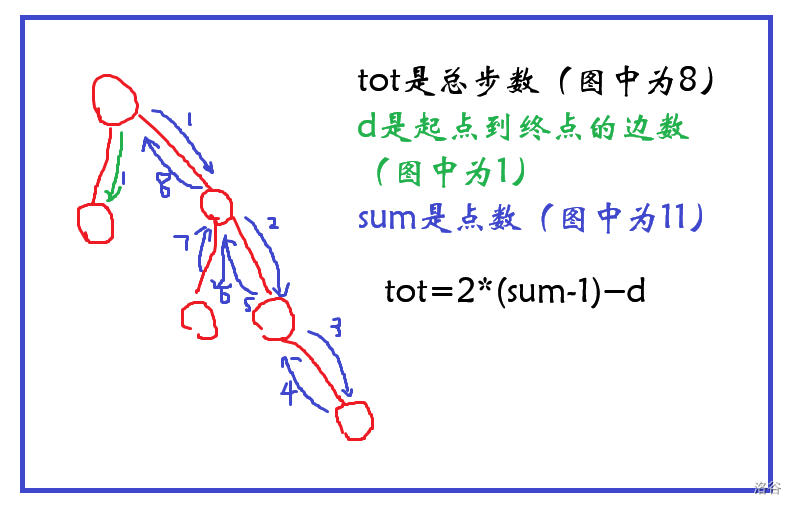
-
然后,考虑分部分的方法,可以进行 的暴力枚举
-
具体操作时,涉及到对所有部分的合并,如将下图中的A树拆分成B的形状,为了使指令串可以处理所有的部分,应将所有部分合并成C,然后找出C的处理步骤数,就是这一拆分下的答案。
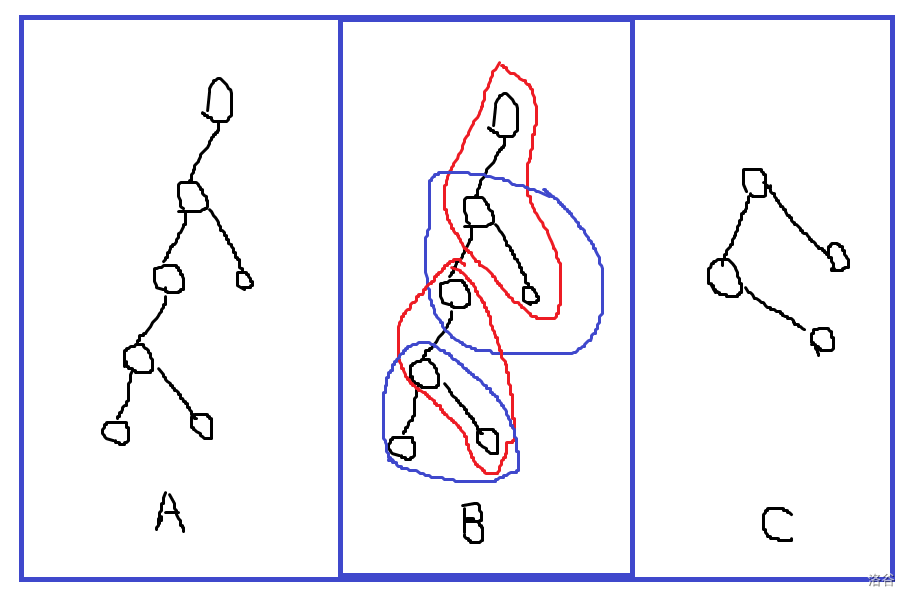
- 最终,答案是所有拆分方法答案中的最小值。
代码实现
1 | |
P5597 【XR-4】复读 题解
http://shicj.pages.dev/2024/02/10/P5597 【XR-4】复读 题解/